4.2 Sampling
When we collect data, it is almost never possible to collect data on the entire population. For instance, if we want to study the habits of people who shop at Checkers, it will not be feasible to send out a survey to everyone in South Africa who has ever shopped at Checkers. When we collect data on a subset of the population, this is called a sample. In cases where we are able to collect data on the whole population, this is called a census. The table below highlights the differences between censuses and samples.
## Warning: package 'knitr' was built under R version 4.3.3| Census | Sample | |
| Definition | A complete enumeration of every individual in a population. | A subset of individuals selected from a population. |
| Coverage | Includes the entire population. | Includes only a portion of the population. |
| Time | Can be very time-consuming due to large-scale data collection. | Requires less time since data is collected on fewer individuals. |
| Cost | Usually quite expensive. | Less expensive. |
| Accuracy | Accurate if data is collected properly, but errors can still occur. | May have some sampling error*. |
| Feasibility | Difficult for large populations. | More practical, especially if the population is large. |
Sampling error will be explained in a later section.
Although it is generally true that more data is better, there are many reasons to take a sample rather than a census. This includes time and financial constraints, as well as feasibility. For example, when taking a geological survey, it is really not feasible to measure the soil at every location in an area! As long as the sample is unbiased and representative, samples can be very informative and helpful.
4.2.1 Sampling Frames
Before we start drawing samples, we must first define the concept of a sampling frame. This is a complete list of all individuals or units in the population of interest from which a sample is drawn. A sampling frame is the foundation for selecting a sample that is representative of the population under study. You can think of a sampling frame as the “pool” from which elements of the sample is drawn.
Example 7: Suppose a market researcher wants to study the shopping habits of students in Pretoria. The population he is interested in are all students at tertiary institutions in Pretoria. The sampling frame would be a complete list of all students currently registered at tertiary institutions in Pretoria.
Exercise: In each of the scenarios given below, describe the population and the sampling frame.
- An animal scientist wants to determine the average weight of male lions in the Kruger Park.
- A human resources professional wants to know the median salary earned by accountants in her company.
- A high school principal wants to identify the best learners in Grade 10 mathematics at his school in 2025.
- A forester wants to wants to estimate the volume of merchantable timber of the pine trees on his plantation.
A good sampling frame must exhibit the following characteristics:
- Completeness: The sampling frame should include every member of the population of interest.
- Accuracy: The information in the sampling frame should be up-to-date and correct.
- No duplicates: Each member of the population should appear exactly once in the sampling frame.
- Relevance: The sampling frame should align with the research question and population of interest.
Exercise: In each of the scenarios given below, evaluate the given sampling frame in terms of its completeness, accuracy, duplicates and relevance.
- A researcher wants to survey registered voters in a city about their voting preferences. They use a voter registration list from two years ago. However, many people have moved away, passed away, or changed their voter registration since then.
- A market researcher wants to study phone usage among adults in a city. They use a landline phone directory as their sampling frame. However, many people, especially young adults, rely exclusively on cellphones and are not listed in the directory.
- A company wants to survey its customers about satisfaction with their products. They use a customer database, but some customers appear multiple times due to different email addresses or accounts (e.g., one customer might have made purchases under both “john.doe@email.com” and “jdoe@work.com”).
- A researcher wants to study pet ownership habits in a city. They use a list of employees from an inner-city corporation as their sampling frame. However, this list only includes people who work at that company, who may not be representative of the broader population (e.g., they may live in flats or complexes that discourage owning pets).
Once a good sampling frame has been constructed, we can proceed with taking a sample. The next two sections will consider different sampling methods.
Important Notation: Note that we will be using \(N\) to denote the population size, and \(n\) to denote the sample size.
4.2.2 Probabilistic Sampling
In probabilistic sampling, every individual in the population has a known and non-zero chance of being selected.
Example 8 (continuation of Example 1): When Raheem collected data from students regarding their campus food preferences, he was collecting a sample, since he was not surveying every single student. There were many ways for him to go about collecting this sample. Here are some of the ways he considered:
- He could have asked his niece Aaliyah, who is studying philosophy, to hand out surveys to her classmates. In this case, only philosophy students who are in Aaliyah’s class would have a non-zero chance of being selected. Engineering students, for example, would have a zero chance of being selected. Thus, this would be a non-probabilistic sample.
- He could have asked one of his friends, John, who is a lecturer in accounting, to hand out surveys to his students. In this case, only accounting students in John’s class would have a non-zero chance of being selected. Philosophy students, for example, would have a zero chance of being selected. Thus, this would be a non-probabilistic sample.
- He could have asked other owners of campus restaurants and food outlets to hand out surveys to their customers. In this case, students who buy food from food outlets on campus would be selected. If Raheem got the owners of all of the outlets on campus to hand out surveys, then all students who buy food on campus would have a non-zero chance of being selected. This would be a probabilistic sample, but NOT of the population Raheem is interested in. Recall that he wanted the opinions of students who do not buy food on campus. Those students would have zero chance of being selected.
- He could have liaised with university management to ensure surveys were sent out to all students via email. In this case, all students would have had a chance to answer the survey. This would be a probabilistic sample.
- He could have asked students to hand out surveys randomly to other students on campus. In this case, all students would, at least in theory, have had a chance to answer the survey. This would be a probabilistic sample.
Example 9: Thabang is a security manager at an airport. In order to reduce airport crime, he wants his staff to search travellers’ luggage. Since all travellers must pass through the security queues, and must also wait in the waiting area at their gate, he could search the luggage of everyone in the security queue, or everyone in the waiting area. However, this is not feasible, as it would take too much time and make people late for their flights. Thus, Thabang knows that he must take a sample of the travellers in the airport. He considers the following options:
- Select all travellers whose surnames begin with an A, an F or an N.
- Generate a sequence of non-repeating random numbers, e.g. 9, 24, 18, etc., and select travellers who are 9th, 24th, 18th, etc. in the security queue.
- Select travellers who are suspiciously in a hurry.
- Select travellers who have red suitcases.
- Select every 10th traveller in the security queue.
- Randomly select travellers from the waiting area at each airport gate.
- Randomly select waiting areas, and search the luggage of all travellers in that waiting area.
Exercise: Discuss each of Thabang’s proposed ways to sample travellers’ luggage, and comment on whether or not this option would constitute a probabilistic sample.

Figure 4.3: Image attribution: Designed by macrovector / Freepik
4.2.2.1 Simple Random Sampling
A simple random sample (SRS) is obtained if each element of the population that has not yet been included in the sample, has an equal chance of being selected in the next draw.
In Example 8, Option 2 is an example of a simple random sample. Here, every person in the security queue who has not yet been selected, has an equal chance of being selected.
Suppose there are 100 people in the queue, i.e. the population size is \(N=100\). Before Thabang generates a random number, each person’s chance of being selected is \[\frac{1}{N}=\frac{1}{100}.\] Now suppose Thabang wants a sample of size \(n=10\). He generates the first random number, 9. The 9th traveller’s luggage is searched, and they are excluded from being searched again. Now, the chance of every other person in the queue being selected is \(\frac{1}{99}.\) Thabang now generates another random number (excluding the number 9), and obtains the number 24. The 24th traveller’s luggage is searched, and they are again excluded from future searches. The chance of every other person in the queue being selected (i.e. everyone except the 9th and 24th travellers) is now \(\frac{1}{98}.\)
This process is repeated until Thabang has sampled as many travellers as he decided on (e.g., 10 travellers).
The procedure to collect a simple random sample is as follows:
- Number all \(N\) elements in the population.
- Decide on a sample size \(n\).
- Select \(n\) random numbers out of the numbers belonging to the population elements.
- Select the population elements corresponding to these random numbers.
The procedure to select random numbers is as follows:
- Select a random starting point from a table of random numbers.
- Divide consecutive single digits into groups, where the size of the groups is the same number of digits as the population size (\(N\)). Write down each of the numbers which is less than or equal to \(N\).
- Include the population elements with numbers that agree with these numbers.
4.2.2.2 Systematic Sampling
In a systematic sample, every \(k\)th element of the population is selected, after a random initial element is selected, where \(k=\frac{N}{n}\). Here, every element of the population has a \(\frac{n}{N}=\frac{1}{k}\) chance of being selected.
In the airport security example, Option 5 represents a systematic sample. Suppose there are now \(N=200\) travellers in the security queue, and that Thabang wants a sample of size \(n=20\). In order to take a systematic sample, he will first calculate \(k=\frac{N}{n}=\frac{200}{20}=10.\) He will then select a random number between 1 and \(k=10\), and select the corresponding traveller in the queue. Say the random number is 3. In this case, he will select the 3rd traveller. Thereafter, he will add \(k=10\) to this random number and select the corresponding traveller, i.e. the 13th traveller. He will repeat the process by selecting the 23rd, 33rd, etc. traveller until the 93rd traveller. He will then have his sample of size \(n=20\).
The procedure to collect a systematic sample is as follows:
- Number all \(N\) elements in the population.
- Decide on a sample size \(n\).
- Calculate the ratio \(k=\frac{N}{n}\), also called the sampling interval.
- Randomly select a number between 1 and \(k\) to determine the first individual in the sample.
- From this starting point, select every \(k\)th individual from the list.
4.2.2.3 Stratified Sampling
In stratified sampling, the population is divided into subgroups (strata), and a random sample is taken from each subgroup (stratum). In the airport security example, Option 6 constitutes stratified sampling. Suppose there are \(3\) waiting areas in the airport. These waiting areas represent the strata. Suppose Area 1 has \(N_1=150\) travellers, Area 2 has \(N_2=100\) travellers, and Area 3 has \(N_3=50\) travellers currently waiting. Thus, the total population size is \(N=N_1+N_2+N_3=300\). If Thabang wants to take a sample of \(n=30\) travellers, he has two different ways to select the sample size per waiting area.
His first option is called proportional stratified sampling, and involves choosing a sample of travellers from each waiting area such that the sample size for each area is proportional to its size in the population. For each waiting area, the sample size can be calculated as \(n_h=\frac{N_h}{N}\times n, h=1,2,3\). Using this formula, he would select \(n_1=\frac{150}{300}\times 30=15\) travellers from Area 1, \(n_2=\frac{100}{300}\times 30=10\) travellers from Area 2, and \(n_3=\frac{50}{300}\times 30=5\) travellers from Area 3. Note that \(n_1+n_2+n_3=30=n\).
His second option is equal stratified sampling, where the same number of individuals is chosen from each stratum, regardless of its size. In this case, \(n_1=n_2=n_3=\frac{n}{3}=\frac{30}{3}=10.\) This kind of sampling is used when it is more important to select the same number of elements from each stratum than to ensure each stratum is represented. In this example, it could lead to Area 1 being under-represented and Area 3 being over-represented in the sample.
The procedure to collect a stratified sample is as follows:
- Number all \(N\) elements in the population.
- Divide the population into mutually exclusive strata. Each individual should belong to one and only one stratum.
- Decide on a sample size \(n\).
- Decide whether to use proportional or equal stratified sampling, and consequently calculate the appropriate sample size per stratum.
- Select a random sample from each stratum using simple random sampling.
Stratified sampling is useful when each stratum is homogeneous, i.e. elements within strata are similar, but there are big differences between strata.
Definition of Homogeneous Data: Homogeneous data consists of elements that are similar or even identical, exhibiting little variation.
Examples:
- Demographics: All of the Grade 11 girls on the netball team at a school. These learners will have the same gender, the same sport, similar ages, weights and heights.
- Environmental data: Measurements of the soil pH of one wetland. The soil pH will not vary so much within one wetland.
- Medical data: All of the women in the maternity ward of a hospital in a high-income area, between the ages of 20 and 30. These women will be similar to each other in terms of income, how many weeks they are due, and will be identical in gender.
- Sales data: The sales records of stationary from the stationary shops in Pretoria. The sales records across all stationary shops will be fairly similar in terms of the products sold (pencils, paper, pens, notebooks, etc.) and the periods during which most sales are made (school supplies at the start of a new term, gifts and wrapping paper during the festive season).
4.2.2.4 Cluster Sampling
In cluster sampling, the population is divided into groups (clusters), similarly to stratified sampling. In stratified sampling, however, individuals are selected from each group, whereas in cluster sampling, the groups are selected randomly. In the airport security example, Option 7 is an example of a cluster sample. The waiting areas represent the clusters. To perform cluster sampling, Thabang would randomly select one or two of the waiting areas. Then, he could either perform one-stage cluster sampling, in which case he would select all of the individuals in each cluster. Or, he could perform two-stage cluster sampling, whereby he would sample random individuals from each cluster using simple random sampling. In one-stage cluster sampling, it may not be possible to select a precise sample size, since the size of the selected cluster(s) will determine the size of the sample. In two-stage cluster sampling, the sample size can be enforced more easily. For example, if he wanted a sample of size \(n=20\), and selected Areas 1 and 2, he could randomly select \(10\) individuals from Area 1 and \(10\) individuals from Area 2.
- Number all \(N\) elements in the population.
- Divide the population into mutually exclusive clusters. Each individual should belong to one and only one cluster.
- Decide on the number of clusters to sample.
- Decide whether to use one-stage or two-stage cluster sampling. If two-stage cluster sampling is selected, decide on a sample size \(n\).
- Select a random sample from each stratum using simple random sampling.
Cluster sampling is useful when each cluster is heterogeneous, i.e. elements within clusters are different from each other, but there are no big differences between clusters.
Definition of Heterogeneous Data: Heterogeneous data consists of elements that are substantially different from each other, exhibiting a considerable amount of variation.
Examples:
- Demographics: All of the learners in a school, from Grade 1 to Grade 12. These learners will differ substantially from each other in terms of gender, age, height, weight and the sports they prefer.
- Environmental data: Soil pH measured across an entire city that has clay-like, sandy and rocky soil. The soil pH will differ substantially based on where in the city each measurement was taken.
- Medical data: All of the patients in the west wing of a hospital that includes maternity wards, oncology, and an emergency room. These patients will differ from each other in terms of their health conditions, age and gender.
- Sales data: Sales records of grocery shops across countries in the northern and southern hemispheres. These sales records will differ vastly in terms of the kinds of food and supplies sold, as well as when which kind of food will be sold. For example, hearty, rich food will sell better in December in the northern hemisphere, and in July in the southern hemisphere; some countries will not sell pork or alcohol products at all, whereas those same products will be very popular in other countries; some countries will sell specific foods during certain festivals, etc.
4.2.2.5 Probabilistic Sampling Summary
No probabilistic sampling method is necessarily always better than another. It is important to select the appropriate sampling method based on the problem you are trying to solve, and the nature of the data. The table below summarises the characteristics of each probabilistic sampling method, and lists some of their advantages and disadvantages.
| Sampling Method | Description | Example | Advantages | Disadvantages |
| Simple Random Sampling (SRS) | Every individual in the population has an equal chance to be selected. | Randomly selecting travellers in the security queue. | Selection bias is minimised; Easy to understand and implement | Difficult for large populations; Risk of underrepresenting some groups |
| Systematic Sampling | After a random start, every kth individual is selected. | Choosing every 10th traveller in the security queue. | Easier and quicker than SRS; Ensures even coverage of the population | May not be fully random if there is an underlying pattern in the data (e.g., if people are queueing such that every 10th person has a large suitcase, only people with large suitcases will be selected) |
| Stratified Sampling | The population is divided into strata, and a random sample is taken from each stratum. | Sampling a proportional number of travellers from each waiting area. | Ensures all groups are represented; Can be more reliable than SRS when strata are very different from each other | Needs a more in-depth understanding of the population to define suitable strata |
| Cluster Sampling | The population is divided into clusters, and entire clusters are randomly selected. In two-stage cluster sampling, samples are taken from the selected clusters. | Choosing waiting areas at random and then selecting all travellers in each selected area. | Practical and cost-effective compared to SRS and Systematic Sampling; Good to use when clusters are naturally occurring groups, e.g. different waiting areas, or schools, or companies | Clusters may not be representative; Naturally occurring clusters will not necessarily be internally heterogeneous but similar to other clusters |
4.2.3 Non-Probabilistic Sampling
Non-probabilistic sampling occurs when individuals are selected based on convenience or judgment. This means that not every individual has a known or non-zero chance of being chosen. This can introduce bias and a lack of representativeness. However, it can be useful in cases where we do not need a random or representative sample, or where it is infeasible to take a probabilistic sample due to limitations of accessibility, and where ease of access to individuals is important.
Here, we will consider three types of non-probabilistic sampling, namely Convenience Sampling, Judgment Sampling and Quota Sampling.
In convenience sampling, individuals are selected based on how easy they are to reach.
Example 10: Suppose an animal scientist is attempting to study lions in a nature park. Attempting to take a probabilistic sample would require knowledge of how many lions are in the park, which might not be known, since lions could die or be born without the scientist’s knowledge. She might instead study those lions who come to drink at a water hole that is accessible by Jeep. This would exclude lions who drink at rivers, or at water holes that are not accessible to her vehicle. However, it may not be possible for her to study lions she cannot access. In this case, convenience sampling would be appropriate, although there is no way of knowing the chance that each lion has to be selected, and some lions have zero chance of being selected.
In judgment sampling, individuals are selected based on experts’ decisions of which individuals would be most useful for the study.
Example 11: Suppose a conference organiser is tasked with assembling a panel to discuss banking in South Africa. Rather than taking a probabilistic sample of the CEOs and other top officers of South African banks, he might choose to invite only those whom he personally believes will make the most meaningful contribution to the discussion. Although this is a non-probabilistic way of sampling, it can be more targeted and effective in certain scenarios.
In quota sampling,individuals are selected to fulfill predetermined quotas for specific subgroups. It ensures that certain characteristics (e.g., age, gender, occupation) are proportionally represented. However, selection within those groups is not random.
Example 12: A survey of school learners might ensure that 20 learners from each grade answer the survey by asking a prefect to go into a classroom of each grade, and handing out the survey to the first 20 learners in each class that want to fill it in. This is a quick and convenient way to ensure that each grade is adequately represented. However, since it is non-probabilistic, the study might still exhibit various kinds of sampling bias. We will talk about sampling bias in the next section.
4.2.4 Sampling Bias
Regardless of the sampling method we plan to use, it is always important to be aware of the dangers of sampling bias. Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others, leading to a sample that is not representative of the entire population. This can distort the results of a study or analysis, making them unreliable or misleading.
Example 13: Caitlyn is the owner of a pet shop called Paws & Whiskers. She wants to gauge whether her customers are satisfied with the range of products stocked in her shop. If she only sends out surveys to customers who purchase dog food, this would systematically exclude all pet owners who have other pets, such as cats, reptiles, rabbits, mice, birds or fish.
There are six types of sampling bias that we will consider.
4.2.4.1 Selection Bias
This type of bias occurs when certain population groups are systematically excluded or underrepresented in the sample. The pet shop example above illustrates selection bias.
Q: What other kinds of selection bias could occur? Who would be excluded if Caitlyn only sent out surveys to customers who made online purchases, or customers with a loyalty card?
4.2.4.2 Voluntary Response Bias
Voluntary response bias takes place when the individuals who participate in a study are self-selected. Typically, this will lead to the inclusion of only those individuals who have strong opinions and want to be heard, and will exclude individuals with more moderate opinions.
If Caitlyn posts her survey on social media, for instance, without encouraging all of her customers to participate, most of the responses will be from customers who are very unhappy, and perhaps a few customers who are extremely happy with her products.
Think about it: how often do you rate deliveries, apps, or other consumer experiences? Most of us will skip the rating step unless we are either very dissatisfied, or extremely happy with the experience.
4.2.4.3 Survivorship Bias
This kind of bias takes place when only “survivors” or of a population are considered, and those who have dropped out or failed are ignored.
Suppose Caitlyn is studying other pet shops to find out what she could do to improve her business. If she only studies successful pet shops, she might conclude that stocking dog food is all she needs to do in order to remain successful. However, this would ignore all of the pet shops who have had to downscale or close - all of whom have stocked dog food! Clearly, she would be in danger of drawing incorrect conclusions.
Another well-known example of survivorship bias occurred during World War II. American researchers were attempting to understand where bomber aircraft were most vulnerable, and reinforce those vulnerable areas to reduce the number of bombers that were being shot down. To do this, they initially studied damaged bombers to see where they had been hit. An example of such a bomber is shown in Figure 3, with the red dots representing bullet holes. However, they soon realised that this was an example of survivorship bias. The bullet holes in the bombers they were studying represented areas where bombers could be shot and still fly well enough to return to base. Bombers that had been hit in other places (like the fuselage) had been shot down over enemy territory, and did not return to base. Based on this, the scientists suggested that the areas should be reinforced that were not damaged on bombers that had returned. The scientists’ ability to understand survivorship bias was thus able to save many pilots’ lives.
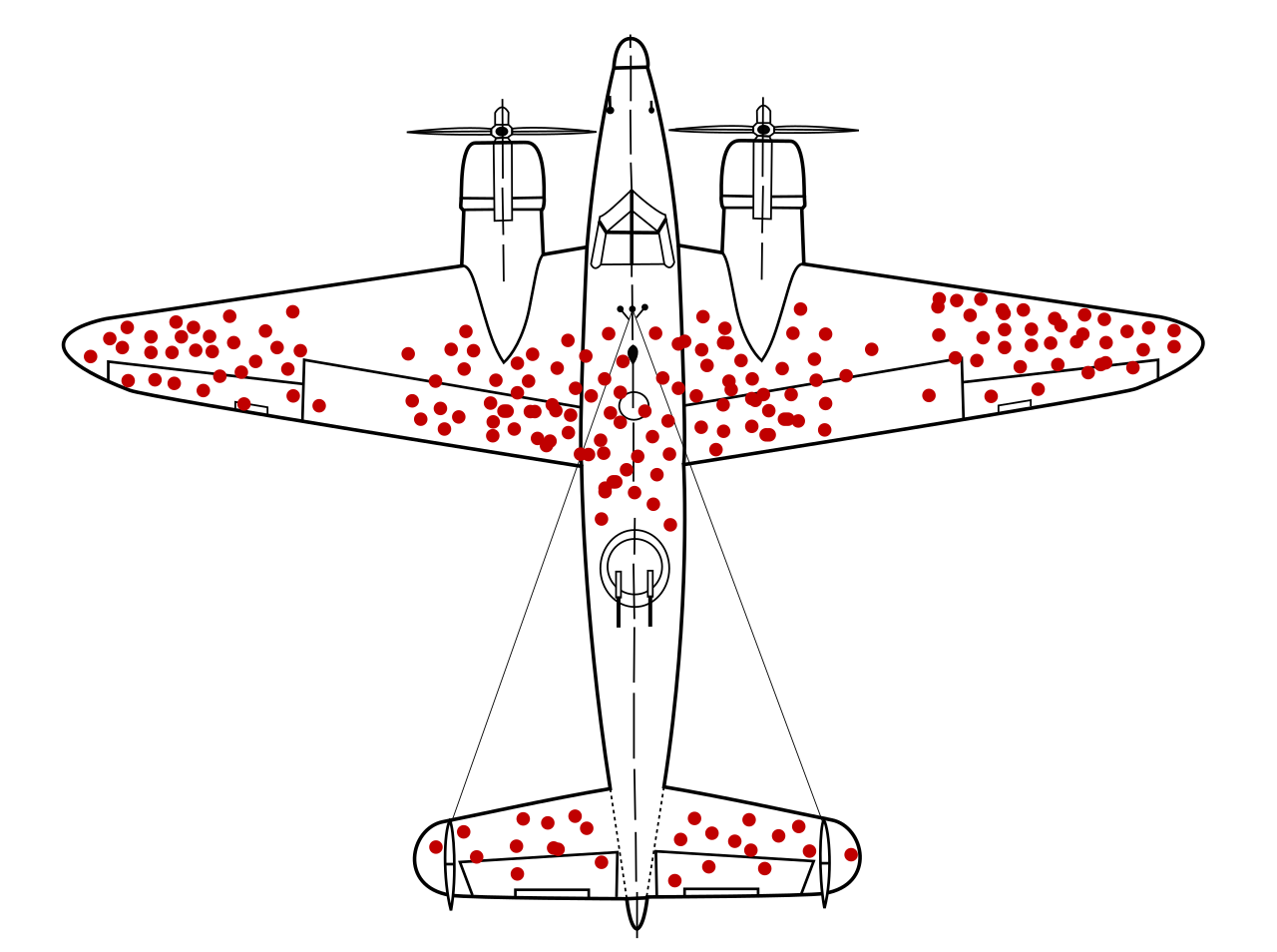
Figure 4.4: Figure 3: Illustration of survivorship bias in World War II planes. Image from Wikipedia: https://en.wikipedia.org/wiki/Survivorship_bias#/media/File:Survivorship-bias.svg/2
4.2.4.4 Time Interval Bias
This bias occurs when the data collected are influenced by the time period during which the sample is collected.
In the pet shop example, time interval bias would occur if Caitlyn collected data on dog jacket sales during summer. She might conclude that dog jackets are not a popular item, when in fact they are very popular in cold weather.
4.2.4.5 Convenience Sampling Bias
As the name suggests, this bias goes hand-in-hand with convenience sampling. When samples are taken only from a group that is easily accessible, this may not represent the general population.
In the pet shop example, Caitlyn might pose questions on her products to customers who are browsing the shop and are not in a hurry. This would be convenient, as she would be talking to relaxed customers who were in a good mood. However, this would exclude all of the customers who were in a hurry, or those who were in a bad mood because they could not find the product they were looking for! In this way, she would not obtain a representative sample of her customers.
4.2.4.6 Non-Response Bias
This kind of bias occurs when there is a substantial difference between individuals who respond to a survey, and those who do not. The effect of non-response bias can be similar to voluntary response bias. The difference is that in voluntary response bias, individuals are not selected in a random way. Thus, individuals are typically excluded if they do not have a strong opinion on the survey. In non-response bias, a proportion of the selected individuals decline to respond.
In the pet shop example, non-response bias could occur if Caitlyn selected a random sample of customers, and then phoned them during work hours. Customers with busy jobs would be more likely to decline her call, whereas those with lower intensity jobs, or those who were not employed, would be more likely to answer her questions.
4.2.4.7 Sampling Bias Summary
In summary, sampling bias can lead to a whole host of errors causing a sample to be unrepresentative of the population. If a researcher assumes that an unrepresentative sample is in fact representative, they could make very incorrect conclusions. These conclusions could be ineffective, or even harmful (the World War II plane example shows just how harmful this can be!).
It is therefore very important to understand and minimise sampling bias as much as possible. Properly designing a probabilistic sample can reduce most types of sampling bias. Additionally, non-response bias can be reduced by following up on those individuals who did not initially respond to the survey.
There are cases where non-probabilistic samples are acceptable for the purpose of the study at hand. However, the researcher must be aware of the fact that their sample does not necessarily reflect the population, and be careful when attempting to apply sample-based conclusions to the population. In the lion example, for instance, it might be acceptable for the researcher to study only those lions who drink at a waterhole that is accessible by Jeep. But, she would have to acknowledge this as a limitation in her study, and be careful of applying her conclusion to all lions. The lions who drink at the waterhole, for example, are able to drink enough water and do not suffer from dehydration. However, it would not be correct of her to assume that all of the lions in the park are properly hydrated, since there might be other lions at other locations in the park who do not have sufficient access to drinking water.
4.2.4.8 Sampling Bias versus Sampling Error
Finally, it is important to distinguish between sampling bias and sampling error. As explained previously, sampling bias occurs when individuals are excluded from the sample in some systematic way. This can be mitigated by improving the sampling design.
Sampling error, on the other hand, is a type of error that happens purely by chance. This error occurs because samples will almost never be perfectly representative of the population.
In the airport security example, Thabang could have a very well-designed sample, but could still miss a traveller who has a dangerous item in their luggage.
In the pet shop example, Caitlyn might conclude that 82% of her customers are satisfied with her products, based on a representative, probabilistic sample. However, the real number based on the population might be 80% or 85%.
The size of the sampling error can be estimated by using statistical techniques. For example, Caitlyn might be able to calculate that there is a 5% fluctuation in her results. In that case, even if the sample indicates that 82% of her customers are satisfied with her products, she will know that the true number could be as low as 77% or as high as 87%.
Nearly all samples will exhibit some degree of sampling error. This can be mitigated by increasing the sample size.
| Type of Error | Sampling Error | Sampling Bias |
| Cause | Random chance | Systematic problem in the sampling method |
| Effect | Estimates will vary slightly | Systematic error in the results |
| How to Mitigate | Increase the sample size | Redesign the study |
| Randomness of Error | Random (cannot be avoided) | Systematic (can be avoided) |
| Severity | Not necessarily severe; will always occur | Very severe - can have harmful consequences unless the study is redone |
| Example | A survey finds that 82% of customers are happy when the true number is 84% | The World War II bomber example |